October 2024 > Math, Algorithms

Large Box Blur using Texture Mipmaps

I remain interested in differential processes for modelling plant vein structures (see here for my first post on the subject). After transitioning my models to OpenGL (via LWJGL) for some much-needed speed enhancements, I still found that large-scale, isotropic blurring was a prohibitive runtime bottleneck.

Like many who first poke around the subject, I immediately ran into the "box blur," which is an image convolution kernel with constant entries. \[ \begin{bmatrix} \alpha & \alpha & \ldots & \alpha \\ \alpha & \ddots & & \vdots \\ \vdots & & \ddots & \alpha \\ \alpha & \ldots & \alpha & \alpha \end{bmatrix} \star f(x,y)\,.\] It is a well-known fact that multiple applications of a box blur approximates a Guassian blur. Moreover, large box blurs can be computed in constant time given an integral image of the original.

Box blurs are separable, which is simply the true statement that \[ \begin{bmatrix} \alpha & \alpha & \ldots & \alpha \\ \alpha & \ddots & & \vdots \\ \vdots & & \ddots & \alpha \\ \alpha & \ldots & \alpha & \alpha \end{bmatrix} \star f(x,y)= \begin{bmatrix} 1\\ 1\\ \vdots \\ 1 \end{bmatrix} \star \begin{bmatrix} 0 & 0 &\ldots & 0 \\ \vdots&\vdots && \vdots \\ 0 & 0 &\ldots & 0 \\ \alpha & \alpha & \ldots & \alpha\\ 0 & 0 &\ldots & 0 \\ \vdots&\vdots && \vdots \\ 0 & 0 &\ldots & 0 \end{bmatrix} \star f(x,y)\,. \] Because convolution ("\(\star\)") is associative, we can first apply a purely horizontal blur, then a purely vertical blur, and achieve the same result as if we had done a full box blur. The end result is that we require two integral images, one for the horizontal component and one for the vertical. More formally, given an image \(f(x,y)\), we require a horizontal integral image \(h(x,y)\) and a vertical integral image \(v(x,y)\) such that \[ \begin{align*} h(x,y) & =\sum_{i=0}^{x-1} f(i,y) \\ v(x,y) &= \sum_{i=0}^{y-1} f(x,i) \end{align*}\,. \]

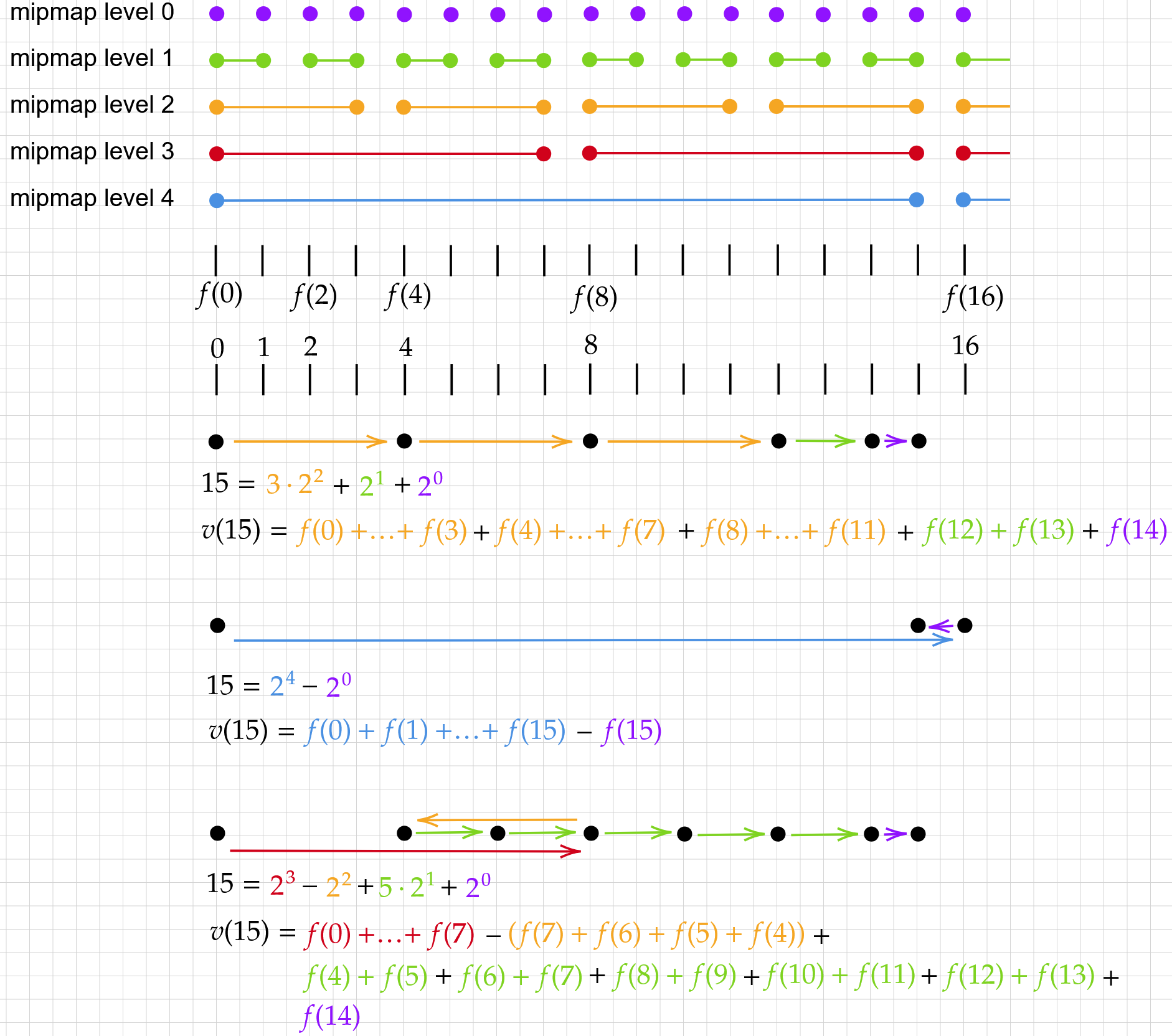
Integral image calculation on a GPU has been done before, perhaps most completely in the 2010 paper Efficient Integral Image Computation on the GPU. Simplifying things to the 1D case, where we seek \(v(x)=\sum_{i=0}^{x-1} f(x)\) (partial sums), the decent methods I have seen build up \(v(x)\) from cached mipmap-like sums \(\sum_{i=2^k}^{2^{k+1}-1} f(\beta 2^k + i)\). For example, \[ \begin{align*} v(15) &= f(0) + f(1) + \ldots + f(14) \\ &= \left(f(0)+f(1)+\ldots+f(7)\right) + \\ &\qquad \left(f(8)+f(9)+\ldots+f(11) \right)+ \\ &\qquad \left(f(12)+f(13)\right) + \\ &\qquad f(14)\,. \end{align*} \] Each of the sub-expressions in parentheses is cached in \(f(x)\) 1D mipmaps. Clever implementations (like the paper linked above) cache more than this to limit redundant sums, for example in \(v(14)\) and \(v(15)\).

This is well and good, but it seems as if we would be better off calculating \(v(15)\) as \[ v(15) = \left(f(0)+f(1)+\ldots+f(15) \right) - f(15)\,. \] Moreover, by allowing subtraction with addition in our cached mipmap values, we could reduce the total operations necessary to generate \(v(j)\) for any \(j\).

Extended Binary Model

Define \(g:\mathbb{N}\to \mathbb{N}\) by \[ g(n):= \inf \left\{ |c_0|+|c_1|+\ldots+|c_k| : n=\sum_{j=0}^k c_j 2^j, \quad c_j\in \mathbb{Z} \right\}\,. \] The number 7, for example, can be written in a number of ways: \[ \begin{align*} 7 &= 7 \times 2^0 \\ 7 &= 2^1 + 5\times 2^0 \\ 7 &= 2^2 + 2^1 + 2^0 \\ 7 &= -1\times 2^1 + 9\times 2^0 \\ 7 &= 2^3 - 2^0\,. \end{align*} \] The sum with the smallest coefficient sum (in absolute value) is \(7 = 2^3 - 2^0\), so \(g(7)=2\). We call this an "extended binary model" because we're representing a number \(n\) in binary, except the binary "digits" can be any integer, not just zero or one. Obviously one loses uniqueness of representation this way!

Of course, \(g(j)\) turns out to be the number of cached mipmap samples that one needs to fetch for \(v(j)\). Powers of two stack up to form \(j\) in the same way that mipmapped partial-sums of \(f\) add up to \(v(j)\).

Any sum can be thought of as traversing the number line starting from \(0\), with positive summands corresponding to rightward motion and negative summands to leftward motion. By associating an integer \(k\) on the number line with the value \(f(k)\), we can generate sums of the form \(\sum_i \pm f(a_i)\), where \(a_i\) is the sequence of integers that we visit, and a negative applied if we visit the number in the leftward (negative) direction. This is how we transform a decomposition \(j=\sum_k c_k 2^k\) into a sum of \(f(k)\) terms. By ordering the summands in \(\sum_k c_k 2^k\) in decreasing powers of \(2\), we can be assured that the \(f\) sum generated by the traversal \(c_k 2^k\) has already been calculated in one of our mipmap levels. This figure gives three examples of decompositions of \(15\) that map to \(f\) sums yielding \(v(15)\).

There are few immediate properties of \(g\).

A minimal sum \(n=\sum_j c_j 2^j\) has \(c_j\in \{-1,0,1\}\) for all \(j\). A "minimal sum" \(\sum_j c_j 2^j\) for \(n\) is one such that \(g(n)=\sum_j |c_j|\).
For any \(n\in\mathbb{N}\), we have \(g(2n)=g(n)\).
For \(n>0\), we have \(g(4n-1)=g(4n+1)=1+g(n)\).
A minimal sum \(n=\sum_{j=0}^k c_{k-j}2^{k-j}\) has partial sums \(\sum_{j=0}^p c_{k-j}2^{k-j}\) contained in the interval \([0, 2^k]\), and \(2^k\) is the smallest power of two greater than \(n\).

For (1), suppose a minimal sum \(n=\sum_j c_j 2^j\) has \(|c_k|>1\) for some \(k\). The \(c_k 2^j\) term can be rewritten \((c_k-2)2^j+2^{j+1}\) if \(c_k>0\), otherwise \((c_k+2)2^j-2^{j+1}\). This means a net decrease in \(|c_1|+|c_2|+\ldots\), a contradiction.

For (2), note that an even \(n\) has \(c_0=0\) in its minimal sum; this follows by taking the residue modulo two of \(n=\sum_j c_j 2^j\) and (1) above. There is thus a bijection \(\sum_j c_j 2^j \leftrightarrow \sum_j c_j 2^{j-1}\) between sums of \(2n\) with coefficients in \(\{-1,0,1\}\) and sums of \(n\) with coefficients in \(\{-1,0,1\}\).

Now onto (3). If \(n=\sum_j c_j 2^j\), we certainly have \(g(4n+1)\leq 1+g(n)\) and \(g(4n-1)\leq 1+g(n)\) since \[ \begin{align*} 4n+1 &= 2^0+4\sum_j c_j 2^j=2^0+\sum_j c_j2^{j+2} \\ 4n-1 &= -2^0 + 4\sum_j c_j 2^j=-2^0+\sum_j c_j 2^{j+2}\,. \end{align*} \] On the other hand, taking the residue modulo four of \(4n+1=\sum_j c_j 2^j\), we arrive at \[ \overline{1}=\overline{c_0}+2\overline{c_1}\,. \] There are two solutions satisfying \(c_0,c_1\in \{-1,0,1\}\) here: \((c_0, c_1)=(1,0)\) and \((c_0,c_1)=(-1,1)\). Since \(c_0+c_1 2^1\) yields the same value in both cases and the former has lower coefficient sum, a minimal sum for \(4n+1\) has \(c_0=1\) and \(c_1=0\). Then \[ 4n+1=1+\sum_{j>1}c_j2^j \implies n= \sum_{j>1}c_j 2^{j-2} \] so that \(g(n)< g(4n+1)\). A similar argument suffices for showing that \(g(n)< g(4n-1)\) (in this case \((c_0,c_1)=(-1,0)\)). Combining these inequalities with \(g(4n+1)\leq 1+g(n)\) and \(g(4n-1)\leq 1+g(n)\) above yields the equality \(g(4n-1)=g(4n+1)=1+g(n)\).

For (4), suppose that \(n=\sum_{j=0}^k c_j 2^j\). If there is a \(2^k\) term such that \(2^{k-1}\geq n\), then \[|n|\geq 2^k-\sum_{j=0}^{k-1} 2^j>2^{k-1}\,,\] a contradiction. This shows that the minimal sum has no terms beyond the next power of two. Now if the partial sum \(\sum_{j=0}^p c_{k-j}2^{k-j}\) exceeds \(2^k\), it must be that the \(2^k\) coefficient is one, and that the next largest (non-zero) coefficient is also one. But in this case the remaining terms cannot make up the distance back to \(2^k\) by geometric sum, so we'd have that \(n\) was not in \([0,2^k]\), a contradiction. The argument for if \(\sum_{j=0}^p c_{k-j}2^{k-j}< 0\) is parallel.

Another interesting fact is when \(n\) is odd, we have \[ g(n)=1+\text{min}(g(n-1), g(n+1))\,. \] This is not so important and easy to prove. I'll leave it as an exercise!

To GLSL Code

We know that \(g(n)\) is the number of mipmap samples that we'll need in order to compute \(v(n)\). Here's some values of \(g\):

This is good news. Ordinarily, we'd require 11 mipmap samples to compute \(v(j)\) through 1024, here we need only 6. The question is whether we can translate this theoretical gain into a practical algorithm. Let's look at how the recurrence relation of \(g\) can be used to find a decomposition for \(v\).

First, we know that \(g(2n)=g(n)\). This is saying that the decomposition problem of \(v(2n)\) is the same as \(v(n)\); it's just a matter of scale. In particular, we know that the decomposition for \(v(2n)\) will not include any single term \((f(j))\), terms will always come in adjacent pairs \((f(j)+f(j+1))\) or larger. We can therefore treat pairs as a single unit, just as if we were considering \(v(n)\).

Next, we have \(g(4n\pm 1)=1+g(4n)=1+g(n)\). This one is simple; the decomposition of \(v(4n-1)\) is \(-(f(4n-1))\) plus the decomposition of \(v(4n)\). Similarly, the decomposition of \(v(4n+1)\) is \((f(4n))\) plus the decomposition of \(v(4n)\).

All in all, this leads to a surprisingly simple texture sampling strategy. Here's a basic fragment shader that computes the horizontal integral image given the image mipmap totals.

#version 460

in vec2 v_texCoord;
layout(location = 0) out vec4 fragColor;

// our image has dimensions 2048 x 2048
uniform sampler2D mipmaps_h[12];

// w = h = 2048
uniform int w;
uniform int h;

void main() {
    // these are the (x,y) coordinates of the current pixel
    int x = int(floor(v_texCoord.x * w));
    int y = int(floor(v_texCoord.y * h));

    float total = 0.0;
    int scale = 1;
    int log2_scale = 0;

    // max number of iterations is 7, empirically determined
    for(int i = 0; i < 7 && x > 0; i++){
        // we have three g(2n)=g(n) tests here so we don't spend extra
        // iterations of the loop repeatedly increasing the scale
        if((x / scale) % 8 == 0){
            scale *= 8;
            log2_scale += 3;
        }
        if((x / scale) % 4 == 0){
            scale *= 4;
            log2_scale += 2;
        }
        if((x / scale) % 2 == 0){
            scale *= 2;
            log2_scale++;
        } else {
            int xs = x / scale;
            if((1 + xs) % 4 == 0){
                total -= texelFetch(mipmaps_h[log2_scale], ivec2(xs, y), 0).x;
                x += scale;
            } else {
                total += texelFetch(mipmaps_h[log2_scale], ivec2(xs - 1, y), 0).x;
                x -= scale;
            }
        }
    }

    fragColor = vec4(total, 0.0, 0.0, 1.0);
}