July 2024 > Math, Algorithms

I. Interval Arithmetic

This is part I of the series A Practical Guide to Boolean Operations on Triangle Meshes.

A friend recently introduced me to a home-spun variant of four square which he called "Thrombus" ("three-rhombus"). Among other changes, Thrombus introduces no-fault line hits: if the ball hits a line between two players, then either player may play the ball legally, and if no player hits the ball, no one is out. This rule has interesting implications for gameplay, but one thing that it doesn't do is alleviate the fundamental perception issue about agreeing in what region the ball landed in.

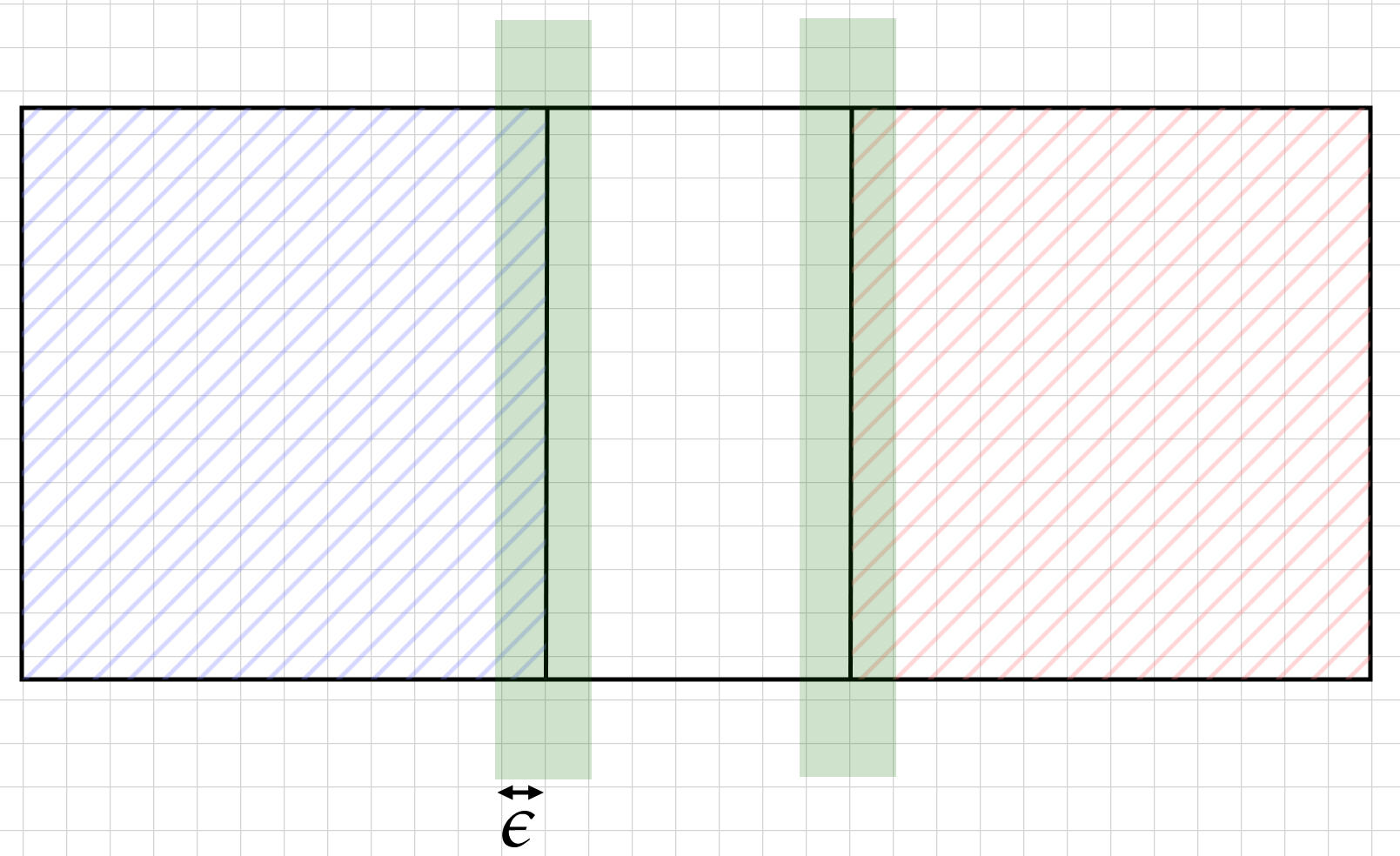
Figure 1: A zoomed-in view of a four-square court, centered on the line separating two players. Player A's region is in blue, to the left, with player B's region in red, to the right. The middle region is "the line," having non-zero thickness.

Figure 1 shows a zoomed-in view of the boundary between two players, with player A on the left, player B on the right, and the line (having thickness, unshaded) in the middle. Human perception is limited, especially from a distance, so no player can perfectly accurately gauge where the ball lands at every given bounce. Supposing that a player's vision is accurate up to \(\epsilon\) — that is, if a player sees the ball land at a particular spot, the ball actually landed within \(\epsilon\) of the spot — there are fundamentally ambiguous regions in which the ball may land. These are shaded in green in Figure 1, and indicate a location where players may disagree about what region the ball lands in (player A's region, the line, or player B's region).

These ambiguous regions are theoretically game breaking, even if in practice it is not so. Even if all players agree that the ball landed in player A's region, they may all be wrong, leading to dramatically different game results. Players may be at odds with each other, each believing the ball landed in a different region, without much (fair) recourse to settle their dispute. Even if we imagine some fancy video-replay system, there is still some error in measuring the exact location of the ball's bounce. So while the frequency of disputed plays may be significantly lessened (think the green region in Figure 1 becoming narrower and narrower), there remains a non-zero probability of the ball bouncing in an ambiguous region.

This is basically the problem of doing geometry with finite-precision floating point numbers. You have some input numbers which are transformed in some way to produce an output. This transformation generates floating point error in the result. Our goal is to classify the result into discrete outcomes and make a decision based on the outcome. But since we can only rarely guarantee zero floating point error, the odds of making a potentially algorithm-ending mistake are non-zero. Just as implementing video replay in four square only reduces the likelihood of an ambiguous ball spot, increasing the precision of floating point numbers (using more digits to represent each number) only reduces the likelihood of an incorrect outcome assignment.

This "likelihood of incorrect outcome assignment" is not something that we can easily quantify and make sufficiently small (as in the case of UUIDs). In the context of the wider boolean operations algorithm, it comes down to the exact coordinates of each triangle in the input meshes. This is outside of our control, and in my experience trying to guess the distribution of input meshes provided by a user is a recipe for disaster. It is generally very easy to come up with reasonable(ish) meshes that result in incorrect outcome assignments for most common geometric tests for any reasonable precision.

An Example: Side-of-Plane Test

The following problem is ubiquitous in computational geometry. Given three non-colinear points \(a\), \(b\), \(c\) defining an oriented plane, determine if a fourth point \(x\) (1) lies on the plane, (2) lies on the positive side of the plane, or (3) lies on the negative side of the plane.

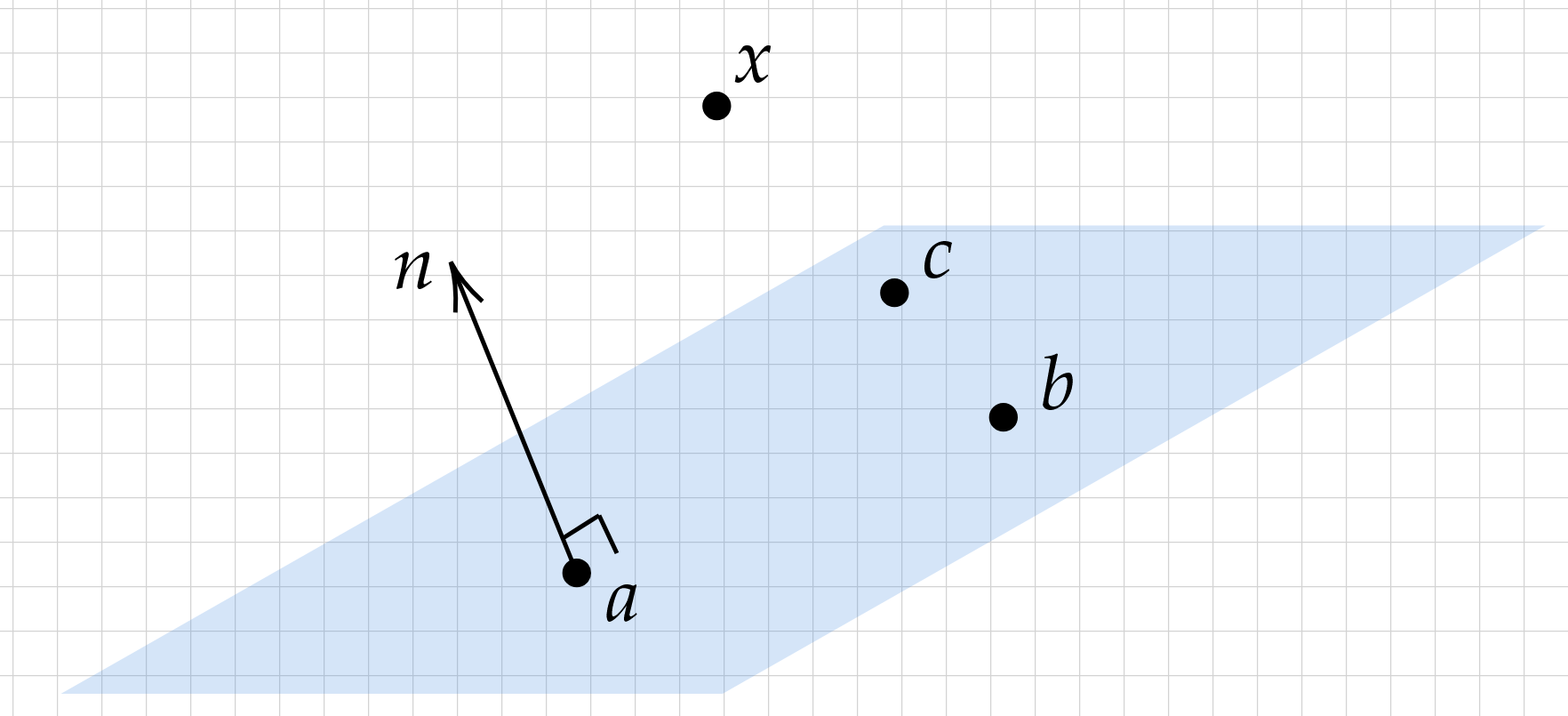
Three non-colinear points \(a\), \(b\) and \(c\) define a plane in 3D. The plane receives an oriented normal vector with direction \(n=(b-a)\times (c-a)\). We want to know whether \(x\) lies on the plane, \(x\) lies on the side of the plane which \(n\) points toward, or \(x\) lies on the side of the plane which \(n\) points away from.

Depending on how smart you want to appear to your friends, you can generate a scalar result quantity \(d\) in several equivalent ways:

By noting that the sign of volume of the oriented parallelpiped formed by \(b-a\), \(c-a\), and \(x-a\) will give us our answer: \(d=\text{det}\left(\begin{bmatrix}b-a& c-a& x-a\end{bmatrix}\right)\)
By remembering the triple product in 3D: \(d=(x-a)\cdot ((b-a)\times (c-a))\)
By re-deriving the triple product using the oriented normal \(n=(b-a)\times (c-a)\) and running the orientation test \(d=(x-a)\cdot n\)

In any case, we transform \(a\), \(b\), \(c\) and \(x\) into a result \(d\). Then we generate a discrete outcome from \(d\) in the following manner: \[ \text{outcome}(d)=\begin{cases} \text{on plane}&\text{if } d = 0 \\ \text{positive side}&\text{if } d > 0 \\ \text{negative side}&\text{if } d < 0 \end{cases}\,.\] According to our characterization of floating point error, there should be values of \(a\), \(b\), \(c\) and \(x\) which produce an incorrect outcome if \(d\) is computed with finite precision. Here's one:

#include <array>
#include <iostream>

using vec = std::array<float, 3>;
float dot(const vec& v1, const vec& v2);
vec cross(const vec& v1, const vec& v2);
vec sub(const vec& v1, const vec& v2);

int main(){
    // Plane is {(x,y,z) : x + y - 2z = 0}
    const vec a = {1.0f, 1.0f, 1.0f};
    const vec b = {-1.0f, -1.0f, -1.0f};
    const vec c = {1.0f, -1.0f, 0.0f};

    // x + y - 2z is -2e-10 here, not zero!
    const vec x = {0.0f, 0.0f, 1e-10f};

    // d = (x - a) . ((b - a) x (c - a))
    const float d = dot(sub(x, a), cross(sub(b, a), sub(c, a)));

    // Our math says that d should not be zero, but floating point arithmetic says otherwise
    std::cout << (d == 0.0f ? "d is zero" : "d is non-zero") << std::endl;

    // Prints "d is zero"

    return 0;
}

float dot(const vec& v1, const vec& v2){
    return v1[0] * v2[0] + v1[1] * v2[1] + v1[2] * v2[2];
}

vec cross(const vec& v1, const vec& v2){
    return {
        v1[1] * v2[2] - v1[2] * v2[1],
        v1[2] * v2[0] - v1[0] * v2[2],
        v1[0] * v2[1] - v1[1] * v2[0]
    };
}

vec sub(const vec& v1, const vec& v2){
    return {v1[0] - v2[0], v1[1] - v2[1], v1[2] - v2[2]};
}

Error Estimation

Geometric tests such as the "side-of-plane" test in the previous section are sometimes called Geometric Predicates. There are relatively straight-forward ways of computing geometric predicates exactly (we'll cover that in another post), but the main issue is that they are very slow. What we can do cheaply is estimate the error associated with floating point arithmetic. Just as in four square, where most of the time everyone can tell that a ball lands in a particular square, most of the time conventional float math will give us the right answer. With error estimation, we can check whether our inputs are in the "problem area" where floating point arithmetic may make a mistake. In fact, there is essentially only one workflow that everyone uses to reliably compute geometric predicates:

Compute the predicate outcome using standard, hardware-implemented floating point arithmetic.
Conservatively estimate the error of step (1).
If the arithmetic error is large enough to possibly affect the result of (1), then go to step (1) with increased precision, OR compute the predicate exactly using other means.

In our previous example (side of plane test), we compute a value \(d\) whose sign tells us which side of the plane \(x\) is on. With error estimate \(\epsilon\) communicating that the theoretical exact value of \(d\) is at most \(\epsilon\)-away from the floating-point calculated value of \(d\), we can conclude that any value of \(d\) found to be within \(\epsilon\) of zero is unreliable. Said another way, our predicate outcome is reliable if \(\{\text{outcome}(d'):d'\in[d-\epsilon,d+\epsilon]\}\) contains only one outcome. If we find our value of \(d\) is unreliable, then we resort to other methods (or increased precision).

Typically, it is rare (\(< 0.1\%\)) that floating point arithmetic is not good enough. We have a vested interest, then, in keeping step (2) as speedy as possible. There are a bunch of methods of error tracking, some more complex than others. But it is difficult to beat the simplicity and flexibility of interval arithmetic, discussed in the next section. In the case of addition, we can use SIMD instructions to perform interval arithmetic error estimation without any performance hit. Other operations have fixed overhead irrespective of the complexity of the hardware instruction, again using SIMD.

I should mention that not everyone thinks that reliable geometric predicates are necessary. There is an interesting class of algorithms which produce consistent but possibly invalid results based on unreliable floating point arithmetic, see A Topologically Robust Boolean Algorithm Using Approximate Arithmetic for example. In this paper, they apply a "data smoothing process" to eliminate invalid results. Ultimately, while interesting, these methods are fundamentally more difficult to reason with because the core algorithms at play aren't 100% reliable. Since they require some post-processing at least (which is very difficult to do robustly), it seems to me unlikely to have much performance benefits.

Interval Arithmetic Basics

The result of a floating point calculation has associated error. Instead of representing the error by some radius \(\epsilon\) as in our side-of-plane example, we calculate bounds \([m, M]\) composed of floating point numbers \(m\) and \(M\) so that the true, mathematically exact result of the calculation lies in the interval \([m,M]\), taken as exact real numbers. For example, there is no floating point number that is exactly equal to \(1+10^{-20}\); instead we substitute the interval \([1,\text{nextFloat}(1)]\) for the result. When we do further calculations, we are applying operations between intervals, not floating point numbers. So \[[1,2]+[3,4]\] should be the smallest interval containing any number \(z=x+y\), where \(x\in[1,2]\) and \(y\in[3,4]\). The minimum possible sum is \(1+3=4\), and the maximum possible sum is \(2+4=6\), so the resulting interval is \([4,6]\).

The simplest way to go about this to exploit IEEE floating point rounding rules together with \(\text{nextFloat}\) and \(\text{prevFloat}\) functions. In this scheme, \[[a,b] + [c,d] = [\text{prevFloat}(a \oplus c), \text{nextFloat}(b \oplus d)]\,.\] Here we use "\(\oplus\)" to refer to the floating-point arithmetic operation to avoid ambiguity. According to the IEEE standard for nearest-rounding (the default option), \(a \oplus c\) is always the nearest floating-point representable value to the mathematical exact value of \(a+c\). Thus \(a+c\) is always larger than the float immediately smaller than \(a\oplus c\) and smaller than the float immediately larger than \(a\oplus c\), equal to \(\text{prevFloat}(a\oplus c)\) and \(\text{nextFloat}(a\oplus c)\) respectively. Similarly, \(b+d\) (the theoretical maximum of the resulting interval) is smaller than \(\text{nextFloat}(b\oplus d)\). Since \(a\oplus c \leq b\oplus d\) when \(a\leq b\) and \(b\leq d\) (this would violate nearest-rounding rules otherwise), we can safely use \(\text{prevFloat}(a\oplus c)\) and \(\text{nextFloat}(b\oplus d)\) as the bounds of our resulting interval.

There is, however, a better way to go about this, which I first learned about from the 2008 paper Fast and Correct SIMD Algorithms for Interval Arithmetic. We can avoid using \(\text{nextFloat}\) or \(\text{prevFloat}\) for addition entirely by setting the rounding mode to "upward" (towards \(+\infty\)). Then \[ [a,b] + [c,d] = [-((-a)\oplus (-c)), b\oplus d]\,. \] Clearly, \(b\oplus d\) is an upper bound for \(b+d\) because of our selected rounded mode. For the minimum bound, note that \((-a) \oplus (-c)\leq (-a) + (-c)\) from our rounding mode. Multiplying both sides by \(-1\) results in \(-((-a)\oplus (-c))\geq -((-a)+(-c))=a+c\). By storing the negation \(-m\) of an interval \([-m,M]\), this addition operation is extra simple: \[ [-a,b] + [-c,d] = [-(a \oplus c), b \oplus d]=[(-a)\oplus (-c), b\oplus d]\,. \] By storing an interval \([-a,b]\) in parallel in a SIMD expanded type, the interval addition is a single instruction, yielding identical runtime to native floating point addition.

SIMD Interval Arithmetic in C++

We will be outlining an SIMD interval arithmetic library for Intel processors with at least SSE2 support. This means we'll be using Intel intrinsics.

Our basic interval unit will be a 4-float wide __m128 type. This can either hold a single interval [-a, b, _, _] with the last two slots unused, or two intervals in parallel [-a, b, -c, d]. Each interval slot contains in the first lane the negation of the minimum bound, and in the second lane the maximum bound. We assume the system adheres to the IEEE 754 standard, and if NaN (signaling or not) or +/-Infinity appears anywhere in an interval, the interval is assumed to represent the entire number line \(\mathbb{R}\). If NaN and +/-Infinity are not present, an interval [-a, b, -c, d] must have \(a\leq b\) and (if a parallel interval) \(c\leq d\).

Some notes:

A 128-bit wide register is the minimum size for interval division to use only one div instruction. If more parallelism is necessary this can be expanded to AVX 256-bit registers without much difficulty, though AVX intrinsics such as _mm256_permute_ps typically have 128-bit lane restrictions.
The IEEE 754 standard is only important insofar as operation tables for non-finite numbers are correct, and the relevant math instructions are accurate up to 1ulp and correctly rounded.
Many interval arithmetic libraries include positive and negative infinity as valid values, so that \([-\infty, 0]\) and \([1,\infty]\) are disjoint intervals for example. They might also support empty intervals \(\varnothing\). While this is admirably complete, it introduces a ton of branching into simple operations. This overhead is excessive for functionality that is only borderline useful; when evaluating geometric predicates anything involving infinity likely means we'll have to redo the calculation using exact arithmetic anyway.

Addition

inline __m128 add(const __m128 a, const __m128 b){
    return _mm_add_ps(a, b);
}

See discussion in "Interval Arithmetic Basics" section. The intrinsic _mm_add_ps adds two four-lane SSE registers as floating point numbers.

Finiteness and well-formed conditions

If a or b is non-finite, then the result is non-finite. This follows from the IEEE addition table.
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). For an intervals [-a, b, _, _] and [-c, d, _, _], we require that \(-((-a)\oplus(-c))\leq b\oplus d\). The LHS is \(a\oplus c\) (floating point arithmetic plays well with sign), and adding our argument requirements \(a\leq b\) and \(c\leq d\) yields \(a\oplus c\leq b\oplus d\), as required.

Parallel version

inline __m128 add_parallel(const __m128 a, const __m128 b){
    return _mm_add_ps(a, b);
}

The intrinsic add works the same across all lanes, so no change is needed for a parallel version.

Performance

Test script:

volatile float res = 0.0f;
volatile __m128 res_i = f32i::interval(0.0f, 0.0f);
// TEST_COUNT = 100,000,000
// a and b are fixed, random floats with a_i and b_i equivalent interval versions (respectively)

// Native addition test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res += a + b;
}
// Interval addition test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_i = f32i::add(res_i, f32i::add(a_i, b_i));
}

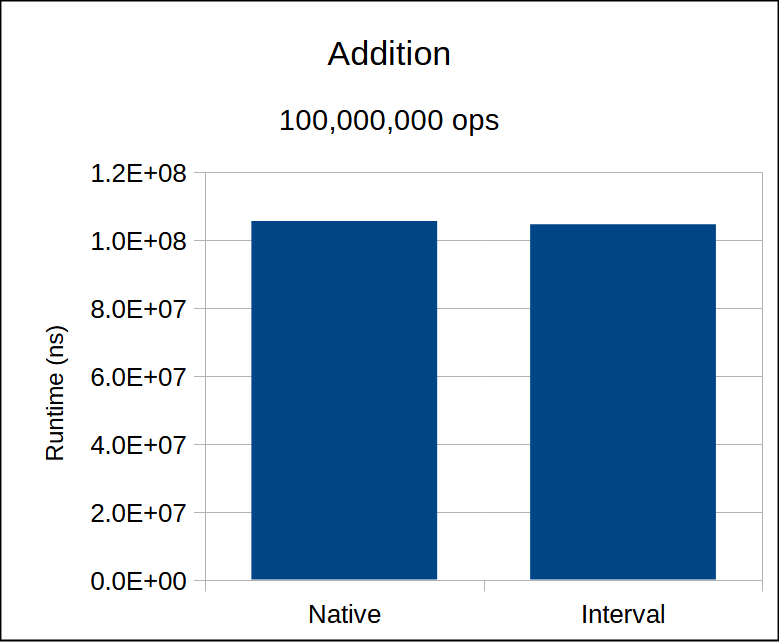
The intrinsic _mm_add_ps compiles to a single add instruction. Performance is identical to native float addition.

Negation

inline __m128 negate(const __m128 a){
    return _mm_shuffle_ps(a, a, _MM_SHUFFLE(2, 3, 0, 1));
}

Negation is an exact operation in floating point arithmetic; we need only flip the sign bit. For a finite interval \([m,M]\), its negation is \([-M, -m]\), so our negate-minimum-bound format saves us an instruction here; we just swap the lanes in the interval. Note that _MM_SHUFFLE(3, 2, 1, 0) is the identity shuffle, which may be backward from your expectation.

Finiteness and well-formed conditions

If a or b is non-finite, then the result is non-finite. Since we are merely swapping the (negated) minimum and maximum, any NaN or infinity will remain in the resulting interval.
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). If [-a, b, _, _] is the representation of the interval \([a,b]\), then \(a\leq b\) so that \(-b\leq -a\) (recalling that floating point negation is exact). This means that [b, -a, _, _] represents a valid interval.

Parallel version

inline __m128 negate_parallel(const __m128 a){
    return negate(a);
}

Notice how we also swapped lanes 3 and 4 in the non-parallel negate, so there is no need for a separate parallel version.

Performance

Test script:

volatile float res_neg = 1.0f;
volatile __m128 res_neg_i = f32i::interval(1.0f, 1.0f);
// TEST_COUNT = 100,000,000

// Native negation test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_neg = -res_neg;
}
// Interval negation test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_neg_i = f32i::negate(res_neg_i);
}

The shuffle intrinsic has latency and throughput similar to an XOR instruction, which is what the usual negation operator resolves to. Note that compiling using later SSE version may result in a vpermilps instruction rather than shufps; these are comparable.

Subtraction

inline __m128 sub(const __m128 a, const __m128 b){
    return add(a, negate(b));
}

Since negation is an exact operation on floating point numbers, this occurs no extra approximation penalty (i.e. wider than necessary interval) over an add call.

Finiteness and well-formed conditions

If a or b is non-finite, then the result is non-finite. If a is non-finite, then the add call will return a non-finite result (see addition section). If b is non-finite, then the negate call will return a non-finite result (see negation section), which will propagate through add.
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). As above, this follows directly from the fact that negate and add satisfy this condition.

Parallel version

inline __m128 sub_parallel(const __m128 a, const __m128 b){
    return add_parallel(a, negate_parallel(b));
}

Not much to say here; note that this is equivalent to add(a, negate(b)).

Performance

Test script:

volatile float res_sub = 0.0f;
volatile __m128 res_sub_i = f32i::interval(0.0f, 0.0f);

// TEST_COUNT = 100,000,000, a is a (pseudo-)random float, a_i is the interval [a, a]
// Native subtraction test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_sub = res_sub - (a - res_sub);
    // loop body assembly:
    // vsubss   xmm1, xmm2, xmm1
    // vsubss   xmm0, xmm0, xmm1
}
// Interval subtraction test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_sub_i = f32i::sub(res_sub_i, f32i::sub(a_i, res_sub_i));
    // loop body assembly:
    // vpermilps   xmm0, xmm0, 177
    // vaddps   xmm0, xmm0, xmm2
    // vpermilps   xmm0, xmm0, 177
    // vaddps   xmm0, xmm0, xmm1
}

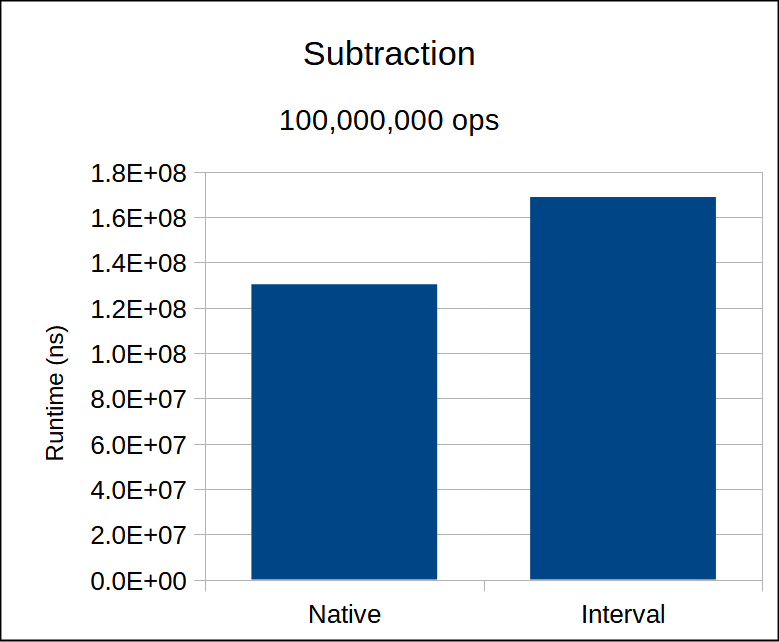
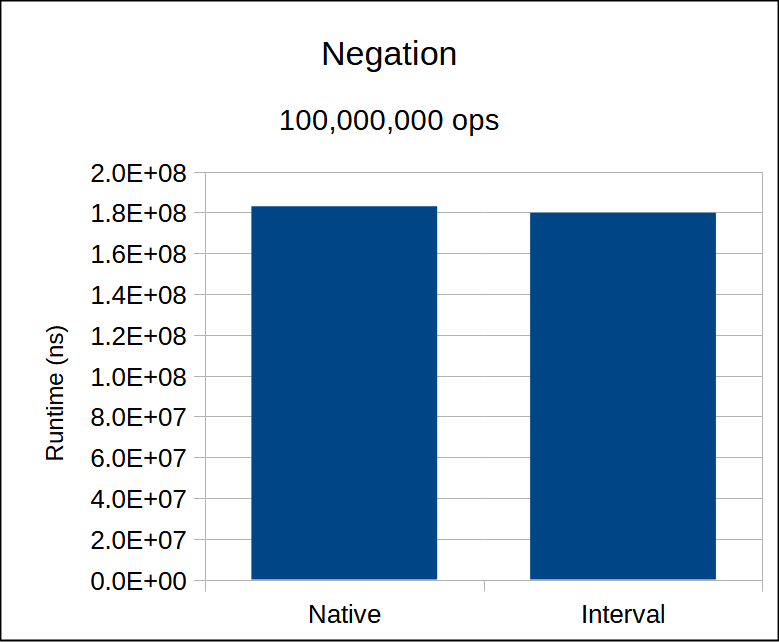
In this particular test it's important to make sure that the -O3 optimization does not mess with the subtraction operation that we're looking for; the relevant assembly is listed in the loop body. The runtime of interval arithmetic is consistently slower than the native version. This is pretty clear from the assembly. What is perhaps surprising is that it is not substantially slower. Recall that vpermilps has significantly less latency than vsubss/vaddps. Since these are all dependent instructions, they cannot be executed in parallel. The upshot is that even though our interval assembly has double the instruction, it should not equate to double the runtime per iteration (in cycles).

Decrement Minimum Bounds (decr_min)

The point of this function is to decrease the minimum component \(m\) in an interval \([m, M]\) to the largest float less than \(m\), or keep \(m\) non-finite if \(m\) is non-finite. Although our rounding mode and minimum component sign means we don't need a "previous float" function for addition and subtraction, this is an important sub-routine for multiplication, division, square root, etc. The rounding mode still helps, however, as we do not need a "next float" function. The basic idea is to re-interpret the float minimum component as an integer, then increment or decrement the integer depending on the sign of \(m\). Some special cases are needed for negative zero and negative infinity.

inline __m128 decr_min(const __m128 interval){
    const __m128i min_max_i = _mm_castps_si128(_mm_add_ps(interval, _mm_set_ps(0.0f, 0.0f, 0.0f, 0.0f)));
    const __m128i ONE = _mm_set_epi32(0,0,0,1);
    const __m128 p = _mm_castsi128_ps(_mm_add_epi32(min_max_i, ONE));
    const __m128 n = _mm_castsi128_ps(_mm_sub_epi32(min_max_i, ONE));
    const float f = _mm_cvtss_f32(interval);
    return f >= 0.0 || f == -INFINITY ? p : n;
}

Let's first understand the bit strings we're working with and where we'd like them to go.

Bit String	Float Value	Goal Bit String	Goal Float Value
1 11111111 11111111111111111111111	-NaN (smallest)	1 11111111 11111111111111111111110	Another -NaN
1 11111111 00000000000000000000001	-NaN (largest)	1 11111111 00000000000000000000000	-Infinity
1 11111111 00000000000000000000000	-Infinity	1 11111111 00000000000000000000001	-NaN
1 11111110 11111111111111111111111	Min finite value	1 11111110 11111111111111111111110	Next largest
1 00000001 00000000000000000000000	Max negative normal	1 00000000 11111111111111111111111	Min negative subnormal
1 00000000 00000000000000000000001	Max negative subnormal	1 00000000 00000000000000000000000	-0.0
1 00000000 00000000000000000000000	-0.0	0 00000000 00000000000000000000001	Min positive subnormal
0 00000000 00000000000000000000000	0.0	0 00000000 00000000000000000000001	Min positive subnormal
0 00000000 11111111111111111111111	Max subnormal	0 00000001 00000000000000000000000	Min positive normal
0 11111110 11111111111111111111111	Max finite value	0 11111111 00000000000000000000000	Infinity
0 11111111 00000000000000000000000	Infinity	0 11111111 00000000000000000000000	NaN (smallest)
0 11111111 00000000000000000000000	NaN (smallest)	0 11111111 00000000000000000000000	Infinity
0 11111111 11111111111111111111111	NaN (largest)	0 11111111 11111111111111111111110	Another NaN

Our minimum interval bound \(m\) is stored in its negated form in the first SIMD slot. In order to decrement \(m\), we increment the first SIMD slot value. We see in the table above that incrementing floating point numbers is a relatively straight-forward procedure, with a few gotchas:

Negative float values require that their bit string (viewed as an integer) be decremented, while positive float values require their bit string incremented.
Positive zero (+0.0) can be incremented as a positive float, but negative zero (-0.0) needs to be incremented by 2.
Non-finite values (NaN and Infinity) need to map to other non-finite values for our finiteness condition. It doesn't matter which ones.

With that in mind, let's walk through the code.

inline __m128 decr_min(const __m128 interval){
    // Note that -0.0 + 0.0 = 0.0 according to IEEE standard; see https://www.cs.uaf.edu/2011/fall/cs301/lecture/11_09_weird_floats.html
    // By adding 0.0, we remove the special case for -0.0. 
    const __m128i min_max_i = _mm_castps_si128(_mm_add_ps(interval, _mm_set_ps(0.0f, 0.0f, 0.0f, 0.0f)));
    // Recall the 1 here, though appearing in the last argument of _mm_set_epi32, initializes the first SIMD slot
    const __m128i ONE = _mm_set_epi32(0,0,0,1);
    // In every case, we either increment the minimum (as an integer) or decrement.
    //   p is the incremented case
    //   n is the decremented case
    const __m128 p = _mm_castsi128_ps(_mm_add_epi32(min_max_i, ONE));
    const __m128 n = _mm_castsi128_ps(_mm_sub_epi32(min_max_i, ONE));
    const float f = _mm_cvtss_f32(interval);
    // This is a subtle comparison. Let's go through the cases here:
    //   f == -NaN: f >= 0.0 is false, f == -Infinity is false, we decrement 
    //   f == -Infinity: f == -Infinity is true, we increment 
    //   f == negative finite: f >= 0.0 is false, f == -Infinity is false, we decrement 
    //   f == -0.0: f >= 0.0 is *true*, we increment. Recall in this case that min_max_i is +0.0, not -0.0 
    //              since we added 0.0 to interval when initializing min_max_i.
    //   f == 0.0: f >= 0.0 is true, we increment
    //   f == positive finite: f >= 0.0 is true, we increment 
    //   f == +Infinity: f >= 0.0 is true, we increment 
    //   f == +NaN, f >= 0.0 is *false* since every comparison with NaN evaluates to false. We decrement.
    // Check with the table above to confirm that these are the correct actions!
    return f >= 0.0 || f == -INFINITY ? p : n;
}

Finiteness and well-formed conditions

If interval is non-finite, then the result is non-finite. The maximum interval bound is unchanged, so if NaN or Infinity is present in the maximum the result will also be non-finite. If the minimum interval bound is non-finite, then f will be one of {-NaN, -Infinity, Infinity, NaN} in the above code. If NaN or -NaN, f >= 0 || f == -INFINITY is false, since any comparison with NaN evaluates to false. Then the bit string of f is decremented, resulting in another NaN, or +/-Infinity. If f == +/-Infinity, then f >= 0 || f == -INFINITY is true and f is incremented, resulting in +/-NaN.
The returned interval \([m,M]\), if finite, satisfies \(m \leq M\). Our input interval [-a, b, _, _] satisfies \(a\leq b\). Since \(a\) is always decreased or turned into a non-finite number, the returned interval [-a', b, _, _] satisfies \(a'\leq b\) if \(a'\) is finite.

Parallel version

inline __m128 decr_min_parallel(const __m128 interval_p){
    const __m128i min_max_i = _mm_castps_si128(_mm_add_ps(interval_p, _mm_set_ps(0.0f, 0.0f, 0.0f, 0.0f)));
    const float f1 = _mm_cvtss_f32(interval_p);
    const float f2 = _mm_cvtss_f32(_mm_permute_ps(interval_p, _MM_SHUFFLE(2, 2, 2, 2)));
    const __m128i diff = _mm_set_epi32(
        0, 
        f2 >= 0.0 || f2 == -INFINITY ? 1 : -1, 
        0, 
        f1 >= 0.0 || f1 == -INFINITY ? 1 : -1
    );
    return _mm_castsi128_ps(_mm_add_epi32(min_max_i, diff));
}

There is nothing particularly inspiring about the parallel version. We do save a couple add instructions over doing two distinct decr_min calls, but that's about it. Note that the two parallel minimum components have no relation between each other; one might be positive and the other negative, or both have the same sign.

Performance

We're not going to do a bar graph like we did with arithmetic operators since there's not a native hardware comparison. However, we can comment on the behavior of this function. First of all, this does not compile to a branchless assembly snippet on my machine (g++ 13.1). While one might expect the ternary to be compiled to a cmov instruction, g++ evidently thought that it was better to save the f == -INFINITY test and n calculation for when f >= 0.0 evaluates to false. It's not immediately clear if this is a branch that is able to be predicted well.

Second, it would be convenient to remove the dependence on -Infinity, since this needs to be loaded from memory or stored in a register. One option is the comparison f + k <= f for some suitable (positive) k. But k needs to be something like MAX_VALUE here, which defeats the purpose of avoiding a large constant. Probably the best option would be to generate the integer matching -Infinity using a few bit operations and then cast. It's not worth testing until we're in a more complex situation; right now the constant -Infinity is kept in a register outside of the test loop.

Minimum/Maximum from Set (min_max)

This is an interesting operation that appears in division. The idea is to take a float-valued SIMD vector [a, b, c, d] and return another vector containing the minimum and maximum values of \(a, b, c, d\). It turns out to be convenient to return [-min(a,b,c,d), max(a,b,c,d), _, _], where "_" indicates an entry that may contain anything. This is useful because it side-steps sign branching; for example \([a,b]\times [c,d]\) could be any of \(\{[ac,bd],[ad,bc],[bc,ad],[bd,ac]\}\) depending on the signs of \(a,b,c\) and \(d\). Instead we can compute the resulting interval as \([\min(ac,ad,bc,bd), \max(ac,ad,bc,bd)]\).

It's extra cool because we only need two _mm_max_ps calls to achieve this, together with some shuffle and logical operators. Let's take a look:

inline __m128 min_max(const __m128 p){
    // The usual way to find max of [a,b,c,d]:
    //   max([a b c d], [b c d a]) = [max(a,b) max(b,c) max(c,d) max(d,a)]
    //  --> permute (1 2 3 4)=>(3 4 1 2) --> [max(c,d) max(d,a) max(a,b) max(b,c)]
    //   max([max(a,b) max(b,c) max(c,d) max(d,a)], [max(c,d) max(d,a) max(a,b) max(b,c)]) has 
    //   all 4 components equal to max(a,b,c,d)
    //
    // This is 3 permute, 2 min, 2 max, 1 blend, 1 xor (all said and done for both max and min)

    // The better way:
    // max([-a, b, -c, d], [-b, a, -d, c]) = [-min(a,b), max(b,a), -min(c,d), max(d,c)]
    //  --> permute                          [-min(c,d), max(d,c), -min(a,b), max(b,a)]
    // max of these is                       [-min(a,b,c,d), max(b,a,d,c), -min(c,d,a,b), max(d,c,b,a)]
    //
    // This is 2 permute, 0 min, 2 max, 0 blend, 2 xor

    // Note unique behavior of max/min for x86: https://www.felixcloutier.com/x86/minps
    // In short, if NaN is an argument to max(a,b), the second argument (b) will be returned, no matter which of {a, b} is NaN.
    // We require that NaN propagates through this function, i.e., if NaN is one of {a,b,c,d}, then NaN must be present 
    // in the first or second component of the result.
    // 
    // If a == NaN, then max(b,a) == NaN and max(d,c,b,a) = max(max(d,c), max(b,a)) == NaN  (last component)
    // if b == NaN, then max(-a,-b) == -NaN and -min(c,d,a,b) = max(max(-c,-d), max(-a,-b)) == -NaN  (2nd to last component)
    // if c == NaN, then max(d,c) == NaN and max(b,a,d,c) = max(max(b,a), max(d,c)) == NaN (2nd component)
    // if d == NaN, then max(-c,-d) == -NaN and -min(a,b,c,d) = max(max(-a,-b), max(-c,-d)) == -NaN (1st component)
    //
    // Recall that NaN values have all 1's in the exponent. So the upshot is that in order to propagate a == NaN and b == NaN,
    // we need to OR the first component with the third and the second with the fourth (+1 permute, +1 or)

    const __m128 a = _mm_xor_ps(p, _mm_set_ps(0.0f, -0.0f, 0.0f, -0.0f)); // [-a, b, -c, d]
    const __m128 b = _mm_xor_ps(_mm_shuffle_ps(p, p, _MM_SHUFFLE(2,3,0,1)), _mm_set_ps(0.0f,-0.0f,0.0f,-0.0f)); // [-b, a, -d, c]
    const __m128 max = _mm_max_ps(a, b);
    const __m128 max_permute = _mm_shuffle_ps(max, max, _MM_SHUFFLE(1,0,3,2));
    const __m128 result = _mm_max_ps(max, max_permute);
    const __m128 nan_permute = _mm_shuffle_ps(result, result, _MM_SHUFFLE(1,0,3,2));

    return _mm_or_ps(nan_permute, result);
}

The most important trick here is that min(a, b) = -max(-a, -b), which is true exactly for floating point numbers. We can then exploit the parallel SIMD _mm_max_ps instruction to compute both the minimum and maximum at once. Of special note is the unusual behavior of _mm_max_ps with regard to NaN. We need to arrange our permutations well so that any NaN present in the original vector makes it to one of the first two components of the result.

Finiteness and well-formed conditions

The finiteness condition is a little different than usual, since min_max doesn't accept an interval. However, we would still like to impose the following: if any of the components to p are non-finite, then a non-finite value must be present in the first two components of the result. A table is perhaps not the most elegant here, but possibly the most convincing:

input	a	b	max	max_permute	result
`[NaN,_,_,_]`	`[-NaN,_,_,_]`	`[_,NaN,_,_]`	`[_,NaN,_,_]`	`[_,_,_,NaN]`	`[_,_,_,NaN]`
`[-NaN,_,_,_]`	`[NaN,_,_,_]`	`[_,-NaN,_,_]`	`[_,-NaN,_,_]`	`[_,_,_,-NaN]`	`[_,_,_,-NaN]`
`[Inf,_,_,_]`	`[-Inf,_,_,_]`	`[_,Inf,_,_]`	`[_,Inf,_,_]`	`[_,_,_,Inf]`	`[_,Inf,_,Inf]`
`[-Inf,_,_,_]`	`[Inf,_,_,_]`	`[_,-Inf,_,_]`	`[Inf,_,_,_]`	`[_,_,Inf,_]`	`[Inf,_,Inf,_]`
`[_,NaN,_,_]`	`[_,NaN,_,_]`	`[-NaN,_,_,_]`	`[-NaN,_,_,_]`	`[_,_,-NaN,_]`	`[_,_,-NaN,_]`
`[_,-NaN,_,_]`	`[_,-NaN,_,_]`	`[NaN,_,_,_]`	`[NaN,_,_,_]`	`[_,_,NaN,_]`	`[_,_,NaN,_]`
`[_,Inf,_,_]`	`[_,Inf,_,_]`	`[-Inf,_,_,_]`	`[_,Inf,_,_]`	`[_,_,_,Inf]`	`[_,Inf,_,Inf]`
`[_,-Inf,_,_]`	`[_,-Inf,_,_]`	`[Inf,_,_,_]`	`[Inf,_,_,_]`	`[_,_,Inf,_]`	`[Inf,_,Inf,_]`
`[_,_,NaN,_]`	`[_,_,-NaN,_]`	`[_,_,_,NaN]`	`[_,_,_,NaN]`	`[_,NaN,_,_]`	`[_,NaN,_,_]`
`[_,_,-NaN,_]`	`[_,_,NaN,_]`	`[_,_,_,-NaN]`	`[_,_,_,-NaN]`	`[_,-NaN,_,_]`	`[_,-NaN,_,_]`
`[_,_,Inf,_]`	`[_,_,-Inf,_]`	`[_,_,_,Inf]`	`[_,_,_,Inf]`	`[_,Inf,_,_]`	`[_,Inf,_,Inf]`
`[_,_,-Inf,_]`	`[_,_,Inf,_]`	`[_,_,_,-Inf]`	`[_,_,Inf,_]`	`[Inf,_,_,_]`	`[Inf,_,Inf,_]`
`[_,_,_,NaN]`	`[_,_,_,NaN]`	`[_,_,-NaN,_]`	`[_,_,-NaN,_]`	`[_,-NaN,_,_]`	`[_,-NaN,_,_]`
`[_,_,_,-NaN]`	`[_,_,_,-NaN]`	`[_,_,NaN,_]`	`[_,_,NaN,_]`	`[_,NaN,_,_]`	`[_,NaN,_,_]`
`[_,_,_,Inf]`	`[_,_,_,Inf]`	`[_,_,-Inf,_]`	`[_,_,_,Inf]`	`[_,Inf,_,_]`	`[_,Inf,_,Inf]`
`[_,_,_,-Inf]`	`[_,_,_,-Inf]`	`[_,_,Inf,_]`	`[_,_,Inf,_]`	`[Inf,_,_,_]`	`[Inf,_,Inf,_]`

We see that the only real problem with returning result is when +/-NaN appears in the first or second SIMD slot of input. This is why we shuffle result and apply an OR operation. In ordinary circumstances, the first/third and second/fourth slot in result is identical, since _mm_max_ps is symmetric in its arguments except when NaN is present. Since _mm_max_ps(x, x) = x, this shuffle-or combo does nothing. But when NaN is present, the all-one exponent of the NaN float in the third or fourth slot will overwrite the exponent in the first or second slot (respectively), causing a NaN to appear in the first two slots as well.

We would also like to apply the well-formed condition to min_max as well, by asserting that the resulting SIMD vector [-a,b,_,_], if finite, always satisfies \(a\leq b\). This is true since min and max are exact operations on finite floating point numbers, with min(a,b,c,d) <= max(a,b,c,d) always.

Performance

As with "Decrement Minimum Bounds", there is no equivalent hardware operation to compare to. However, this is a branchless algorithm thanks to _mm_max_ps.

Maximum from Set (max_h)

We want to take a SIMD vector [a, b, c, d] and return another SIMD vector [M, M, _, _], where M is the maximum value of a, b, c and d. This is exactly the same code as min_max, but with every _mm_xor_ps call stripped out.

// If p = [a,b,c,d], puts max(a,b,c,d) into the first two components of the result
inline __m128 max_h(const __m128 p){
    // [a, b, c, d]
    const __m128 a = p;
    // [b, a, d, c]
    const __m128 b = _mm_shuffle_ps(p, p, _MM_SHUFFLE(2,3,0,1));
    // [max(a,b), max(b,a), max(c,d), max(d,c)]
    const __m128 max = _mm_max_ps(a, b);
    // [max(c,d), max(d,c), max(a,b), max(b,a)]
    const __m128 max_permute = _mm_shuffle_ps(max, max, _MM_SHUFFLE(1,0,3,2));
    // [max(a,b,c,d), max(b,a,d,c), max(c,d,a,b), max(d,c,b,a)]
    const __m128 result = _mm_max_ps(max, max_permute);
    // [max(c,d,a,b), max(d,c,b,a), _, _]
    const __m128 nan_permute = _mm_shuffle_ps(result, result, _MM_SHUFFLE(1,0,3,2));

    return _mm_or_ps(nan_permute, result);
}

Since the primary concern with propagating NaN is the order of arguments in _mm_max_ps (see min_max), ignoring the negation has no effect on NaN propagation.

Finiteness and well-formed conditions

The well-formed condition does not apply here, since an interval is not returned. However, we do wish to apply a version of the finiteness condition. In particular, for an SIMD vector [a, b, c, d] containing any non-finite value, we wish the result vector [M, M, _, _] to contain a non-finite value in its first two components. Moreover, if b or d is non-finite, then the first component of the result will be non-finite. If a or c is non-finite, then the second component of the result will be non-finite.

The proof for this is identical to that of min_max, but with various sign changes not affecting the result. Please refer to the relevant "Finiteness and well-formed conditions" section.

Performance

This is strictly faster than min_max, since it is also branchless and avoids several _mm_xor_ps calls.

Multiplication

inline __m128 mult(const __m128 a, const __m128 b){
    // [-w, x, -w, x]
    const __m128 wxwx = _mm_shuffle_ps(a, a, _MM_SHUFFLE(1,0,1,0));
    // [-y, z, -z, y]
    const __m128 yzzy1 = _mm_xor_ps(_mm_shuffle_ps(b, b, _MM_SHUFFLE(0,1,1,0)), _mm_set_ps(-0.0f, -0.0f, 0.0f, 0.0f));
    // [y, -z, z, -y]
    const __m128 yzzy2 = _mm_xor_ps(yzzy1, _mm_set_ps(-0.0f, -0.0f, -0.0f, -0.0f));

    // [wy, xz, wz, xy]
    const __m128 m1 = _mm_mul_ps(wxwx, yzzy1);
    // [-wy, -xz, -wz, -xy]
    const __m128 m2 = _mm_mul_ps(wxwx, yzzy2);

    return _mm_blend_ps(max_h(m2), max_h(m1), 2);
}

The multiplication function \(\times:\mathbb{R}^2 \to \mathbb{R}\) is continuous, so the image of the connected set \([a,b]\times [c,d]\) is also connected; i.e. an interval. Since multiplication is an open mapping, the endpoints of the resulting interval lie in the set \(\{ac,ad,bc,bd\}\). This is the main idea of the algorithm used above. We can use the four SIMD lanes to compute all endpoint possibilities at once. Since the resulting set is connected, the endpoints must be \(\min(ac,ad,bc,bd)\) and \(\max(ac,ad,bc,bd)\).

Now since these exact products may not be float-representable, we generate an over-approximation via _mm_mul_ps(wxwx, yzzy1); recall that our default rounding mode is toward +Infinity. The negation of an under-approximation is _mm_mul_ps(wxwx, yzzy2), which is just [a*(-c), b*(-d), a*(-d), b*(-c)]. This works the same as addition does: a rounding mode toward +Infinity when working with negated values is the same as a rounding mode toward -Infinity. Similarly, the maximum taken on negated values is the same as a minimum. (More formally, \(\max(-a,-b)=-\min(a,b)\).) Since m2 is a (negated) under-approximation of the endpoint products, its maximum value (really a minimum) represents the negation of an under-approximation to the smallest endpoint product, i.e. the first component of the result. Likewise, m1 is an over-approximation of the endpoint products, so that its maximum is an over-approximation of the largest endpoint product; the second component of the result.

Finiteness and well-formed conditions

If a or b is non-finite, then the result is non-finite. Suppose +/-Infinity or +/-NaN is present in the first two slots of a (the only slots containing meaningful information). Then wxwx also contains a non-finite slot, since it is a shuffle of a. Since any multiplication involving +/-Infinity or +/-NaN returns a non-finite value (see this table), both m1 and m2 will contain a non-finite value. Importantly, m1 and m2 will contain non-finite values in the same SIMD slot. This means that, by the finiteness contract of max_h, max_h(m1) and max_h(m2) will both have a non-finite value in the same slot. This means that any blending of max_h(m1) and max_h(m2) will have a non-finite value in one of the first two SIMD slots. The case for b non-finite is entirely analogous, noting that negation (xor with -0.0) maps non-finite values to non-finite values.
The returned interval \([m,M]\), if finite, satisfies \(m \leq M\). Since max_h(m2) is (the negation of) an under-approximation of the minimal endpoint product and max_h(m1) is an over-approximation of the maximal endpoint product, we have -max_h(m2) <= max_h(m1) in the first two components. The final SIMD vector is formed by taking the first slot of max_h(m2) together with the second slot of max_h(m1), so our condition is satisfied.

Parallel version

inline __m128 mult_parallel(const __m128 a, const __m128 b){
    const __m128 first_lane = mult(a, b);
    // if a = [s,t,u,v], swap_parallel(a) is [u,v,s,t]
    const __m128 x = swap_parallel(a);
    const __m128 y = swap_parallel(b);
    const __m128 second_lane = swap_parallel(mult(x, y));
    return _mm_blend_ps(first_lane, second_lane, _MM_SHUFFLE(1, 1, 0, 0));
}

Since mult takes up all the SIMD slots, we can't do much other than serially perform the multiplications in each lane. This may be a good opportunity for 256 bit SIMD types.

Performance

Test script:

volatile float res_mul = 0.5f;
volatile __m128 res_mul_i = f32i::interval(.5f, .5f);
const __m128 ONE_POINT_ONE_I = f32i::interval(1.1f, 1.1f);

// TEST_COUNT = 100,000,000
// Native multiplication test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    // this will display oscillating behavior, which is good enough for us
    res_mul = 1.1f - res_mul * res_mul;
}

// Interval multiplication test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_mul_i = f32i::sub(ONE_POINT_ONE_I, f32i::mult(res_mul_i, res_mul_i));
}

We use the subtraction to create oscillating behavior for res_mul.

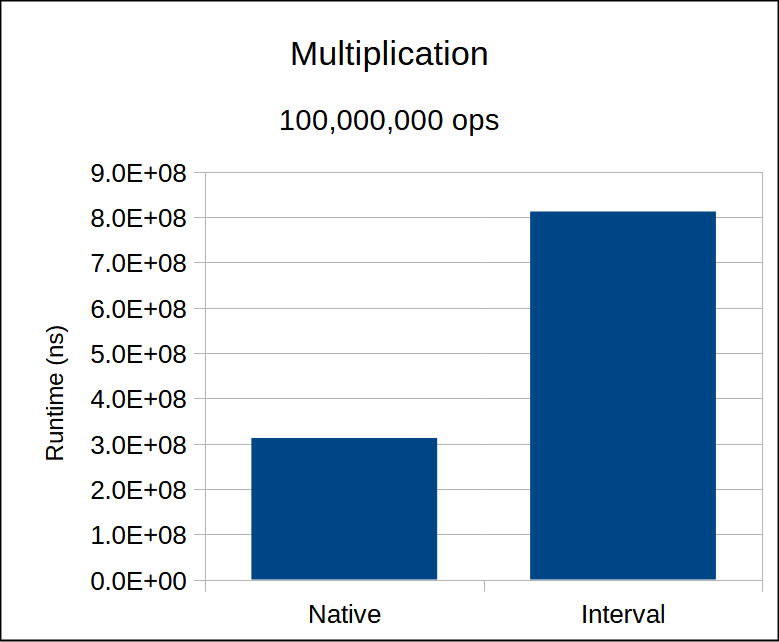
This is going to be our worst relative performance difference across the board. Whereas float division is relatively expensive, multiplication is almost as fast as addition and subtraction. (On my architecture is has the same throughput but higher latency). So there is no hiding the sizable overhead of max_h.

One might be tempted to replace the two _mm_mult_ps calls with a single one (computing only the over-approximation) and use decr_min instead of two max_h calls. This would be the resulting code:

inline __m128 mult_alt(const __m128 a, const __m128 b){
    // [-w, x, -w, x]
    const __m128 wxwx = _mm_shuffle_ps(a, a, _MM_SHUFFLE(1,0,1,0));
    // [-y, z, -z, y]
    const __m128 yzzy = _mm_xor_ps(_mm_shuffle_ps(b, b, _MM_SHUFFLE(0,1,1,0)), _mm_set_ps(-0.0f, -0.0f, 0.0f, 0.0f));
    const __m128 p = _mm_mul_ps(wxwx, yzzy); // [wy, xz, wz, xy] rounded to +inf

    // min_max will always preserve NaN and +/-inf
    const __m128 mm = min_max(p);
    return decr_min(mm);
}

This is not a branchless algorithm due to decr_min, which is a bummer, and it is also measurably slower. The two _mm_mul_ps calls in the non-alt version don't depend on each other and can be queued up at the same time; multiplication has high throughput. min_max also has a fairly high number of negations, so two max_h calls is not necessarily the loss that it appears.

Division

inline __m128 div(const __m128 a, const __m128 b){
    // [-w, x, -w, x]
    const __m128 wxwx = _mm_permute_ps(a, _MM_SHUFFLE(1,0,1,0));
    // [-y, z, -z, y]
    const __m128 yzzy = _mm_xor_ps(_mm_permute_ps(b, _MM_SHUFFLE(0,1,1,0)), _mm_set_ps(-0.0f, -0.0f, 0.0f, 0.0f));
    // [w/y, x/z, w/z, x/y] rounded to +inf
    const __m128 q = _mm_div_ps(wxwx, yzzy); 

    const __m128 mm = min_max(q);
    const __m128 min_max_res = decr_min(mm);

    const float ny = _mm_cvtss_f32(yzzy);
    const float z = _mm_cvtss_f32(_mm_shuffle_ps(b, b, _MM_SHUFFLE(1, 1, 1, 1)));
    constexpr float n_inf = -INFINITY;
    const bool condition = z > n_inf && z < INFINITY && ny > n_inf && ny < INFINITY && (ny < 0 || z < 0);

    return condition ? min_max_res : _mm_set_ps(INFINITY, INFINITY, INFINITY, INFINITY);
}

The function \((x,y)\mapsto x/y\) is continuous on \(\mathbb{R}\times (\mathbb{R}\setminus \{0\})\) and, like multiplication, an open mapping on \(\mathbb{R}\times (0,\infty)\) and \(\mathbb{R}\times (-\infty, 0)\). Thus for the division \([a,b]/[c,d]\) where \(0\notin [c,d]\), the resulting interval is \[ [\min(\frac{a}{c}, \frac{a}{d}, \frac{b}{c}, \frac{b}{d}), \max(\frac{a}{c}, \frac{a}{d}, \frac{b}{c}, \frac{b}{d})]\,. \] Conveniently, when \(0\in [c,d]\), the division function is either unbounded or undefined. In these cases we return a non-finite interval.

We compute the pairwise quotients \(\frac{a}{c}, \frac{a}{d}, \frac{b}{c}, \frac{b}{d}\) in one go, with the result in q. We then compute the minimum and maximum pairwise quotient (mm), and pad the lower bound by 1ulp so our resulting interval is conservative. Then we test whether \(0\in [y,z]\), noting that y is finite exactly when y > -Infinity && y < Infinity; when y == +/-NaN all comparisons evaluate to false. If it is the case that \(0\in [y,z]\), we return a non-finite interval, otherwise our bounded interval calculated from the pairwise quotients.

Finiteness and well-formed conditions

If a or b is non-finite, then the result is non-finite. We'll be referencing the IEEE division table here, for your reference. If a = [w, x, _, _] is non-finite, then q will be non-finite by our division table. In this case, min_max_res is non-finite because of the finiteness contract of min_max and decr_min. Then the returned interval is always non-finite no matter the value of condition. If, on the other hand, b = [y, z, _, _] is non-finite, then condition is false because it explicitly checks that y and z are finite (remember that any comparison with NaN evaluates to false). Then the non-finite interval [Inf, Inf, _, _] is returned.
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). If the returned interval is finite, it must be that condition is true. But since min_max and decr_min satisfy well-formed conditions (see their respective sections), min_max_res is always a well-formed interval.

Parallel version

inline __m128 div_parallel(const __m128 a, const __m128 b){
    const __m128 first_lane = mult(a, b);
    // if a = [s,t,u,v], swap_parallel(a) is [u,v,s,t]
    const __m128 x = swap_parallel(a);
    const __m128 y = swap_parallel(b);
    const __m128 second_lane = swap_parallel(div(x, y));
    return _mm_blend_ps(first_lane, second_lane, _MM_SHUFFLE(1, 1, 0, 0));
}

As with multiplication, since div uses all our SIMD slots, our only real option is to perform both operations serially. This is a good opportunity for 256 bit SIMD vectors, for example.

Performance

Test script:

// TEST_COUNT = 100,000,000
volatile float res_div = 0.5f;
volatile __m128 res_div_i = f32i::interval(.5f, .5f);
const __m128 ONE_POINT_ONE_I = f32i::interval(1.1f, 1.1f);

// Native division test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_div = 1.1 + 1.1f / res_div;
}

// Interval division test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_div_i = f32i::add(ONE_POINT_ONE_I, f32i::div(ONE_POINT_ONE_I, res_div_i));
}

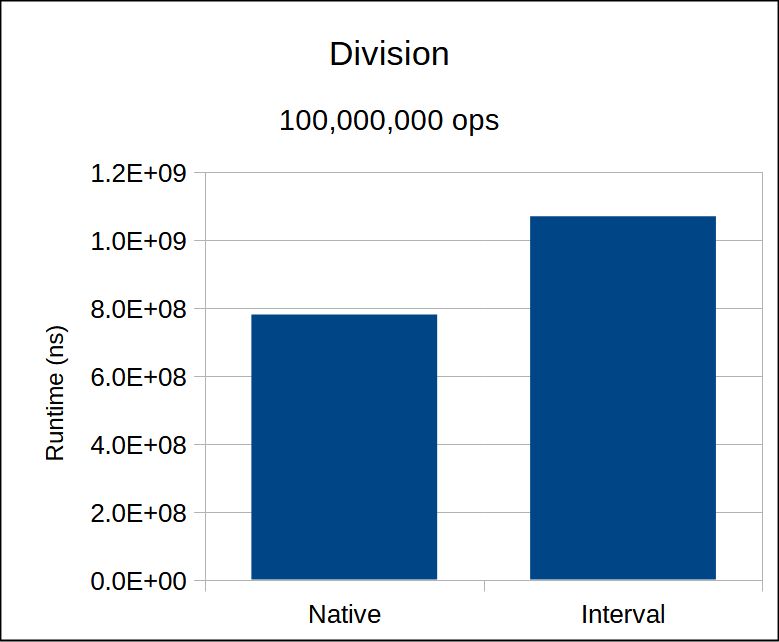
As with multiplication, we have the option of doing two (SIMD) division operations with opposite sign, or one division with decr_min. In this case, tests showed that decr_min is the faster choice. This is not a branchless algorithm, and is the only elementary arithmetic operation (addition, subtraction, multiplication, division) to have branches. Since native division is also relatively slow, this is not as big of a deal.

Absolute Value

Absolute value as a map \(\mathbb{R}\to\mathbb{R}\) is not an open mapping. This is a fancy way of saying that we can't just take the absolute value of the endpoints of an interval and call it a day. Instead, an interval \([a,b]\) has absolute value \([0,b]\) if \(0\in [a,b]\), and an interval \([a,b]\) has absolute value \([-b,-a]\) if \(b < 0\). This branching has to be present (in some form) in the algorithm we choose.

inline __m128 abs(const __m128 a){
    const bool min_neg = _mm_cvtss_f32(a) > 0; // not a typo
    const __m128 shuffled = _mm_permute_ps(a, _MM_SHUFFLE(3,2,0,1));
    const __m128 res = min_neg ? shuffled : a;
    const bool includes_origin = min_neg && (_mm_cvtss_f32(res) > 0);
    if(!includes_origin){
        return res;
    } else {
        const float all_ones = _mm_cvtss_f32(_mm_castsi128_ps(_mm_set_epi32(-1, -1, -1, -1)));
        const __m128 and_mask = _mm_set_ps(all_ones, all_ones, all_ones, 0.0f);
        return _mm_and_ps(_mm_max_ps(a, res), and_mask);
    }
}

The branching is fairly straight-forward for an interval \([m, M]\):

If \(M\leq 0\), then \(\text{abs}([m,M])=[-M,-m]\).
If \(m\geq 0\), then \(\text{abs}([m,M])=[m,M]\).
Otherwise, \(\text{abs}([m,M])=[0,\max(-m, M)]\).

These follows from the fact that the absolute value function is a continuous, open mapping (separately) on \((-\infty,0]\) and \([0,\infty)\). This is fairly straight-forward in the above code. First we assume that the interval a does not contain zero, and set res to the corresponding absolute value based on the sign of the minimal endpoint. As with negation, since we store the negation of the minimal endpoint in the first SIMD component, permutation of the SIMD indices is sufficient to retrieve the negated interval (shuffled). Note that we keep the unused indices 2 and 3 unshuffled for use in abs_parallel.

Then we check whether a contains zero (includes_origin) with a little trick. If min_neg is false, then the minimum component of a is positive and the interval does not contain zero. If min_neg is true, then we need to check that the maximum component of a is positive, but in this case res already contains the maximum component; we can access it with the instruction-less _mm_cvtss_f32 rather than another shuffle call.

In the event that the interval a does contain zero, we use a _mm_max_ps instruction to put \(\max(-m, M)\) into the second SIMD component, and zero out the first component with an _mm_and_ps instruction. (Note that the integer -1 in two's complement is the bitstring consisting of all ones.)

Note that this is an exact algorithm; negation on floating point arithmetic is exact.

Finiteness and well-formed conditions

If a is non-finite, then the result is non-finite. Suppose the interval a has minimal endpoint m and maximal endpoint M. If m is +/-NaN or +Infinity, then min_neg is false, since every comparison with NaN evaluates to false. Then res is returned, which is just a (which contains +/-NaN). If m is -Infinity and includes_origin is false, then res contains +Infinity in its second slot (due to the permutation), which is returned. If m is -Infinity and includes_origin is true, then res has +Infinity in its second slot, _mm_max_ps(a, res) contains +Infinity in its second slot. This is unaffected by the subsequent _mm_and_ps call and returned. If M is +/-NaN or -Infinity, then _mm_cvtss_f32(res) > 0 always is false (if it gets there) so that res is returned. Since res is a permutation of a, M is present in the result. Finally, if M is +Infinity and includes_origin is true, then _mm_max_ps(a, res) contains +Infinity in the second SIMD slot, which propagates to the returned value. (Note that _mm_max_ps works with infinity, see here).
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). If includes_origin is true, then res is either a or the negation of a, both of which satisfy \(m\leq M\). If includes_origin is false, then the returned interval is [0, max(M, -m)] such that \(M \geq 0\) (otherwise includes_origin would be false).

Parallel version

Because absolute value requires basically no computation, only branching, there is not much we can do in the way of a true parallel version.

inline __m128 abs_parallel(const __m128 a){
    // relies on the fact that abs(...) does not change the parallel channel
    const __m128 a_abs_half = abs(a);
    return swap_parallel(abs(swap_parallel(a_abs_half)));
}

Because our absolute value function does not mess with the 3rd and 4th SIMD slots (this is something that needs to be checked carefully), we can skip the blend step typical in "serial" parallel versions like division.

Performance

Test script:

volatile float res_abs = 1.0f;
volatile __m128 res_abs_i = f32i::interval(1.0f, 2.0f);
// TEST_COUNT = 100,000,000

// Native test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_abs = std::abs(res_abs);
    res_abs = std::abs(-res_abs);
}
// Interval test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_abs_i = f32i::abs(res_abs_i);
    res_abs_i = f32i::abs(f32i::negate(res_abs_i));
}

The fact that absolute value is a branching algorithm makes it difficult to accurately test. For one, it's quite difficult to fool the branch predictor (i.e., make branch prediction not essentially 100%) without adding excessive runtime overhead. Even if we could, it's quite possible that the dependency chain is shallow enough in a test like this to not make a difference. For this test, we exercise two branches of f32i::abs, one where the interval is entirely negative and one where it is entirely positive. Since interval arithmetic is designed to primarily work with small intervals, we expect the third branch (the interval contains zero) to be rare; hence its omission from the test case.

We find a very comparable runtime to the native version.

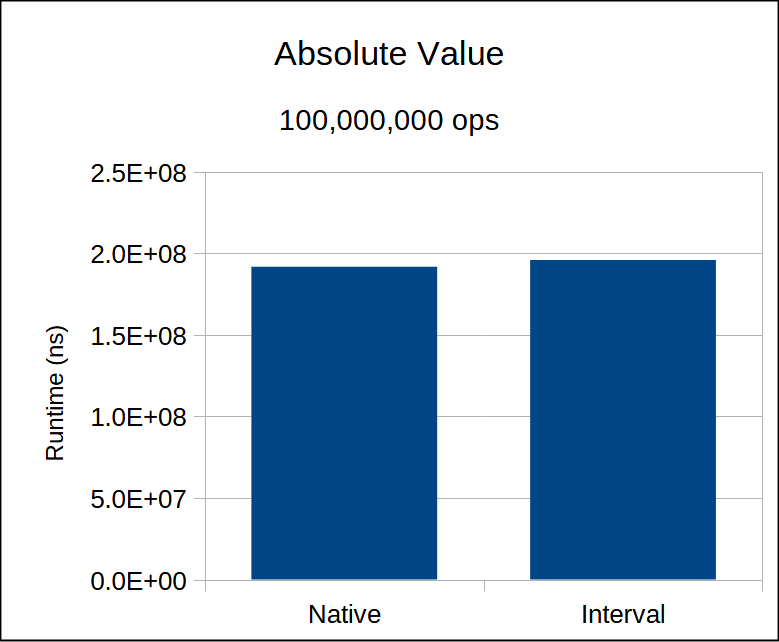
Square

One might be tempted to implement a square function as

inline __m128 sq(const __m128 a){
    return mult(a, a);
}

This yields a much wider interval than we wish. Consider a = [-2, 2]. In this implementation, the returned interval is [-4, 4], but we really know that the square of any real number is positive. The correct interval is [0, 4]. In addition, we can avoid the max_h calls from mult since we know more about the arguments, namely that mult(a, a) has the same second argument as first.

With some thought, you'll notice that the required branching here is very similar to absolute value. Indeed, since \(x^2=\|x\|^2\) and \(x\mapsto x^2\) is monotonic (increasing) on \(\{x\geq 0:x\in \mathbb{R}\}\), we can abstract all our casework to abs.

inline __m128 sq(const __m128 a){
    const __m128 a_abs = abs(a);
    const __m128 sign_flip = _mm_set_ps(0.0f, 0.0f, 0.0f, -0.0f);
    const __m128 a_abs_n = _mm_xor_ps(a_abs, sign_flip);
    return _mm_mul_ps(a_abs_n, a_abs);
}

The SIMD vector a_abs is [-m, M], where [m, M] is the interval representing the absolute value of a. Then a_abs_n is [m, M], by using an xor to flip the sign of the first slot. Our result is then [-m*m, M*M]. Since \(0\leq m \leq M\) from the absolute value call, \(m^2\leq M^2\) and this is the interval we are looking for. Note in particular that both M*M and (-m)*m are rounded upward (our default rounding mode is always to +Infinity), meaning that the bounds are conservative on both sides.

This function never returns an interval containing a negative value. This is because the floating-point multiplication of a non-negative number with a non-positive number is always non-positive.

Finiteness and well-formed conditions

If a is non-finite, then the result is non-finite. The abs function adheres to the finiteness condition, xor with +/-0.0f preserves (the classes) +/-NaN and +/-Infinity, and the multiplication tables for IEEE multiplication preserve +/-NaN and +/-Infinity.
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). If a_abs is the interval [m, M], then the resulting SIMD vector returned is [(-m)*m, M*M, _, _]. Since \(m\leq M\) from the well-formed condition of abs, we see that \(m^2\leq M^2\), noting that IEEE multiplication is monotonic.

Parallel version

inline __m128 sq_parallel(const __m128 a){
    const __m128 a_abs = abs_parallel(a);
    const __m128 sign_flip = _mm_set_ps(0.0f, -0.0f, 0.0f, -0.0f);
    const __m128 a_abs_n = _mm_xor_ps(a_abs, sign_flip);
    return _mm_mul_ps(a_abs_n, a_abs);
}

We can effectively and trivially parellelize everything except the abs call.

Performance

Test script:

volatile float res_sq = 0.5f;
volatile __m128 res_sq_i = f32i::interval(0.5f, 0.5f);
// TEST_COUNT = 100,000,000
// ONE_POINT_ONE_I is initialized to f32::interval(1.1f, 1.1f)

// Native test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_sq = 1.1f - res_sq * res_sq;
}
// Interval test
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_sq_i = f32i::sub(ONE_POINT_ONE_I, f32i::sq(res_sq_i));
}

This is the same test as multiplication, since it already squared a number. See the "Performance" section for multiplication for details.

We achieve significantly better (relative) performance for sq than for mult, which makes sense.

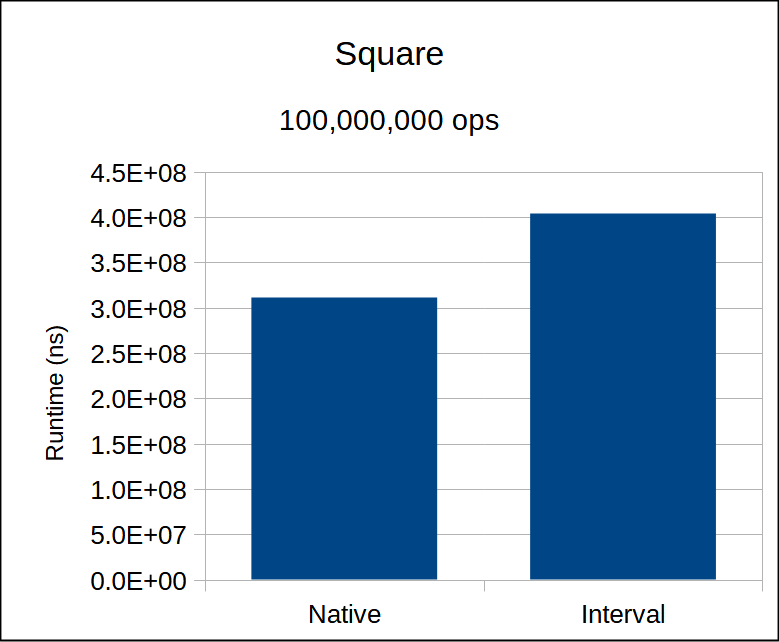
Square Root

This is the first function which has a limited domain over \(\mathbb{R}\). We ought to be careful with this; if we give up on a calculation \(\sqrt{[a,b]}\) when \(a<0\) (say be returning \([-\infty, \infty]\)), we run the risk of the following calculation yielding non-useful results: \[ \sqrt{([a,b]\oplus [c,d])\ominus [c,d]\ominus[a,b]}\,. \] Our strategy will be to only offer functions defined on \(\mathbb{R}\). There are several ways to extend the square root function to \(\mathbb{R}\). We choose \(x\mapsto \sqrt{|x|}\).

inline __m128 sqrt_abs(const __m128 a){
    const __m128 a_abs = abs(a);
    // Flip sign of minimum so we can apply simd sqrt; if a_abs = [-A, B, _, _],
    // then correct_sign = [A, B, _, _]. Both A and B are non-negative here from the abs(a) call above.
    const __m128 sign_flip = _mm_set_ps(0.0f, -0.0f, 0.0f, -0.0f);
    // -0.0f is 1 000000000 0000000000000000000000 so that xor with -0.0 flips the first (sign) bit.
    const __m128 correct_sign = _mm_xor_ps(a_abs, sign_flip);
    // apply sqrt (recall we're on rounding mode to +inf, so this OVERestimates the lower bound by at most 1ulp)
    const __m128 sqrt = _mm_sqrt_ps(correct_sign);
    // swap sign back and decrement min
    return decr_min(_mm_xor_ps(sqrt, sign_flip));
}

Note that abs will always return an interval with non-negative minimum and maximum since abs is an exact operation. Thus correct_sign will always consist of non-negative values so that _mm_sqrt_ps never returns NaN (on finite input).

Since \(x\mapsto \sqrt{x}\) is a monotonically increasing, continuous open mapping on \([0,\infty]\), we can just apply a square root operation to each interval endpoint; i.e., \[ \sqrt{[a,b]}=[\sqrt{a},\sqrt{b}] \] when \(a,b\geq 0\).

It's also important to note that square root (along with addition, subtraction, multiplication and division) is a "basic operation" required by the IEEE standard to be accurate up to 0.5ulp for all inputs.

Finiteness and well-formed conditions

If a is non-finite, then the result is non-finite. Since abs adheres to the finiteness condition, if a is non-finite, then so is a_abs and correct_sign (since changing the first bit of NaN or Infinity results in NaN or infinity). Now sqrt also has this finiteness property, as does decr_min, so if correct_sign is non-finite, then so is the result.
The returned interval \([m,M]\), if finite, satisfies \(m\leq M\). a_abs is always well-formed by abs well-formed condition. This means that correct_sign is the SIMD vector [A, B, _, _] with A <= B. Since we assume that the hardware implementation of SQRT is monotonic and accurate to 1ulp, the result is [-sqrt(A), sqrt(B), _, _] such that sqrt(A) < sqrt(B).

Parallel version

inline __m128 sqrt_abs_parallel(const __m128 a){
    // this is exactly the same as sqrt_abs, except we use decr_min_parallel instead and make sure to apply abs to both channels
    const __m128 a_abs = abs_parallel(a);
    const __m128 sign_flip = _mm_set_ps(0.0f, -0.0f, 0.0f, -0.0f);
    const __m128 sqrt = _mm_sqrt_ps(_mm_xor_ps(a_abs, sign_flip));
    return decr_min_parallel(_mm_xor_ps(sqrt, sign_flip));
}

Performance

Test script:

volatile float res_sqrt = 0.5f;
volatile __m128 res_sqrt_i = f32i::interval(0.5f, 0.5f);

// TEST_COUNT = 100,000,000
// Native test:
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_sqrt = std::sqrt(res_sqrt);
}
// Interval test:
for(std::size_t i = 0; i < TEST_COUNT; ++i){
    res_sqrt_i = f32i::sqrt_abs(res_sqrt_i);
}

Note that we do not check the branching on abs around zero; just as with the performance benchmark for absolute value, we expect the computation \(|[a,b]|\) where \(0\in [a,b]\) to be rare.

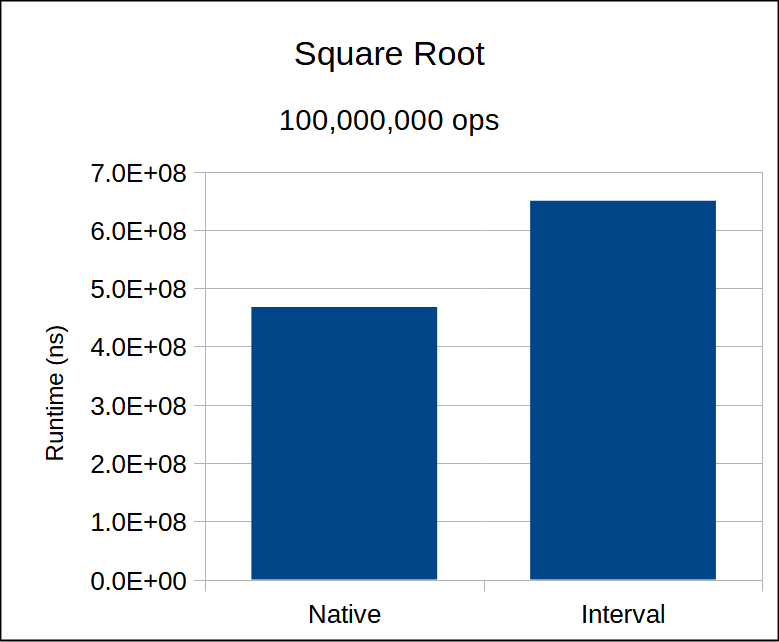
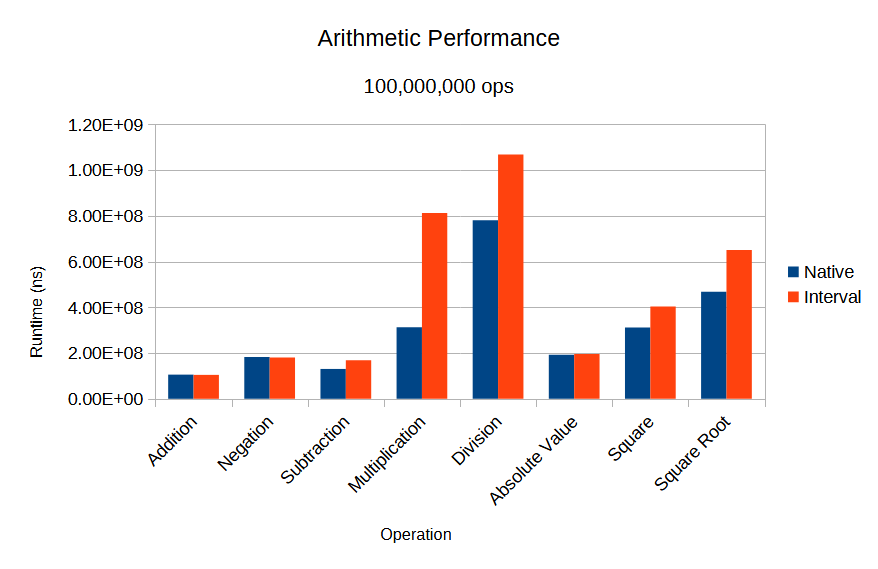
Performance summary, per operation: